本帖最后由 仗剑天涯 于 2023-12-22 18:29 编辑

High-level Synthesis (HLS) has become popular since it can improve the productivity of circuit designs. The optimization of HLS is necessary since the design space is vast and different configurations can lead to various power, performance and area (PPA). In this paper, we model the design space exploration (DSE) as a multi-objective black-box optimization problem via Bayesian optimization with float encoding method to explore the Pareto front of HLS designs for PPA objectives, where Multi-objective Tree-structured Parzen Estimator (MOTPE) is adopted as the surrogate model to search the tree-structured design space efficiently and Expected Hypervolume Improvement (EHVI) is used as the acquisition function to guide the optimization. The experimental results show the outstanding performance of our method compared with two meta-heuristic algorithms, simulated annealing (SA) and NSGA-II. The learned Pareto front by our method is closer to the reference Pareto front than SA and NSGA-II, with an average improvement in ADRS by 94.72% and 69.58% respectively.

Paper Title: Multi-objective Design Space Exploration for High-Level Synthesis via Bayesian Optimization Paper Link: DOI: 10.1109/ISEDA59274.2023.10218665 Code Link: https://github.com/hzkuang/HLSDSE #01 BACKGROUND High-Level Synthesis (HLS) can automatically translate high-level programming languages, such as C/C++, to low-level hardware description languages (HDLs) under the guidance of HLS directives, which makes it possible for users who are not experts in HDLs to describe their circuit designs. It has become a prevailing technology to develop ASIC and FPGA designs. Given different HLS directive configurations, the hardware architectures generated from the same high-level language description can vary significantly from each other, leading to diverse PPA gains. Thus, the Design Space Exploration (DSE) of HLS is necessary to find the Pareto optimal configurations that optimize the design objectives in the entire design space. Though HLS can facilitate the circuit designs, some challenges still hinder researchers from finding the optimal designs efficiently. First, the design space of HLS directive configurations is vast which can grow with the scale of HLS applications. Second, the HLS directives and the design objectives (e.g., power, performance, area) are in a complicated non-linear relationship. Furthermore, it is difficult to balance multiple design objectives which are correlated and conflicted with each other. Therefore, the DSE of HLS directive configurations is a multi-objective optimization problem (MOOP) to optimize multiple objectives simultaneously. 2.1 Tree-structured Design Space Modeling For HLS applications, since some directive configurations are conflicted with others, we develop a general method to model the design space in a tree-structured manner which can automatically avoid invalid configurations. The HLS directives can be divided into four types: Function, Loop, Array, and Operation. Table 1 presents the directives and their options. Table 1: The HLS directive design space For general matrix multiplication (gemm), there are 7 loop parameters, 12 array parameters, 5 int operation parameters and 2 double operation parameters with their parameter combinations in Fig. 1(a) when N in factor is set to 4, which constitutes a vast design space with 2.94×10^10 (2^1×2^3×3^3×3^12×2^5×2^2) configurations in total while some of them are invalid. Fig. 1(b) shows how to model nested loops (L1, L2, L3) of gemm in a tree-structured manner to remove invalid configurations, which can reduce directive configurations to 5.92×10^9 (87×3^12×2^5×2^2). Loop L1 can be flattened since it is a perfect loop, which corresponds to the green circle and the on edge in blue. All three loops can be pipelined (blue circles and on edges) or unrolled (orange circles and on edges) but the directives of loop L3 depend on loops L1 and L2. For example, if loop L2 is pipelined in a configuration, loop L3 has to be fully unrolled automatically, which means it is not necessary to search L3 directives in this case. If a loop is unrolled with a specified integer factor, it corresponds to a black edge. Each path ending up with a blank circle corresponds to a specific configuration, where the parameters in an example path1 within the grey dashed box are active parameters and the grey number (such as #9) represents the number of parameter combinations.
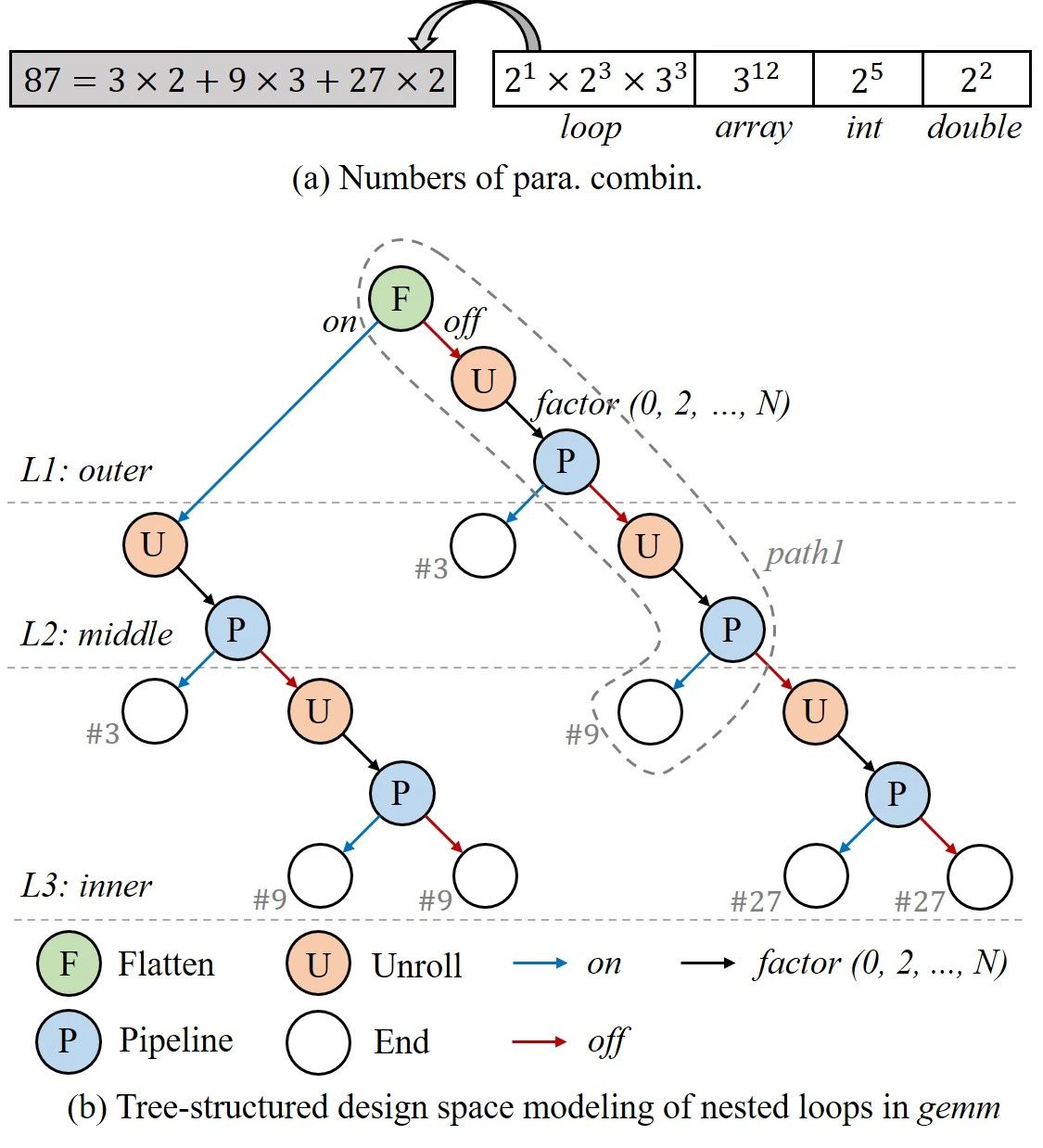
Fig. 1: An example of design space modeling 2.2 Directive Encoding To model the design space in a unified manner, the directive parameters are encoded as float values in [0, 1], which can facilitate the convergence of optimization objectives. The active parameter value can be obtained through an index generated by scaling to the size of the directive option range with downward rounding, which then can be converted to a corresponding directive description. A group of active directives is called a configuration. Fig. 2 shows the directive encoding method and how to combine the directives into one configuration. For instance, when the function inline parameter is set to a float value (such as 0.2), which can be encoded to an index (math.floor(0.2×3) = 0) through multiplying by 3 with downward rounding since this directive has 3 options. Then it ends up with an option (on) corresponding to the index 0. Finally, all the active directives generated in this way are combined and saved to a Tcl script to guide the HLS process.
Fig. 2: An example of the directive encoding method 2.3 The Design Space Exploration Flow Bayesian optimization is adopted as the framework to explore Pareto optimal HLS configurations, with MOTPE as the surrogate model and EHVI as the acquisition function. The overall DSE flow is present in Fig. 3. 1) Design Space Setup At this stage, all the possible locations of directives and their options are specified in two Yaml files, config.yaml and params.yaml, respectively. In consideration of generality, the directive locations are configured with hierarchical tags. 2) Optimization Flow After the design space setup, the DSE engine reads the Yaml files and the application code to perform optimization. The initial set is obtained by random sampling with FPGA flow to get the post-implementation PPA values. At each iteration, the sampled set is split into Dl and Dg first, then the BO algorithm traverses all the active parameters in a tree-structured manner to fit probability model l(x) on Dl and g(x) on Dg. For each active parameter, the best point x∗ is selected from nc candidates to evaluate. After all the active parameters are sampled, PPA values are available from the FPGA implementation flow. Then the sampled set is updated to move on to the next optimization step. When the stopping criterion is satisfied, the Pareto solutions are returned. It is worth mentioning that no training dataset is required and the design space is not determined statically but is define-by-run in the form of a tree. The initial design space of an application can be specified by users via configuration files (Yaml files) based on the characteristics of target FPGA devices.
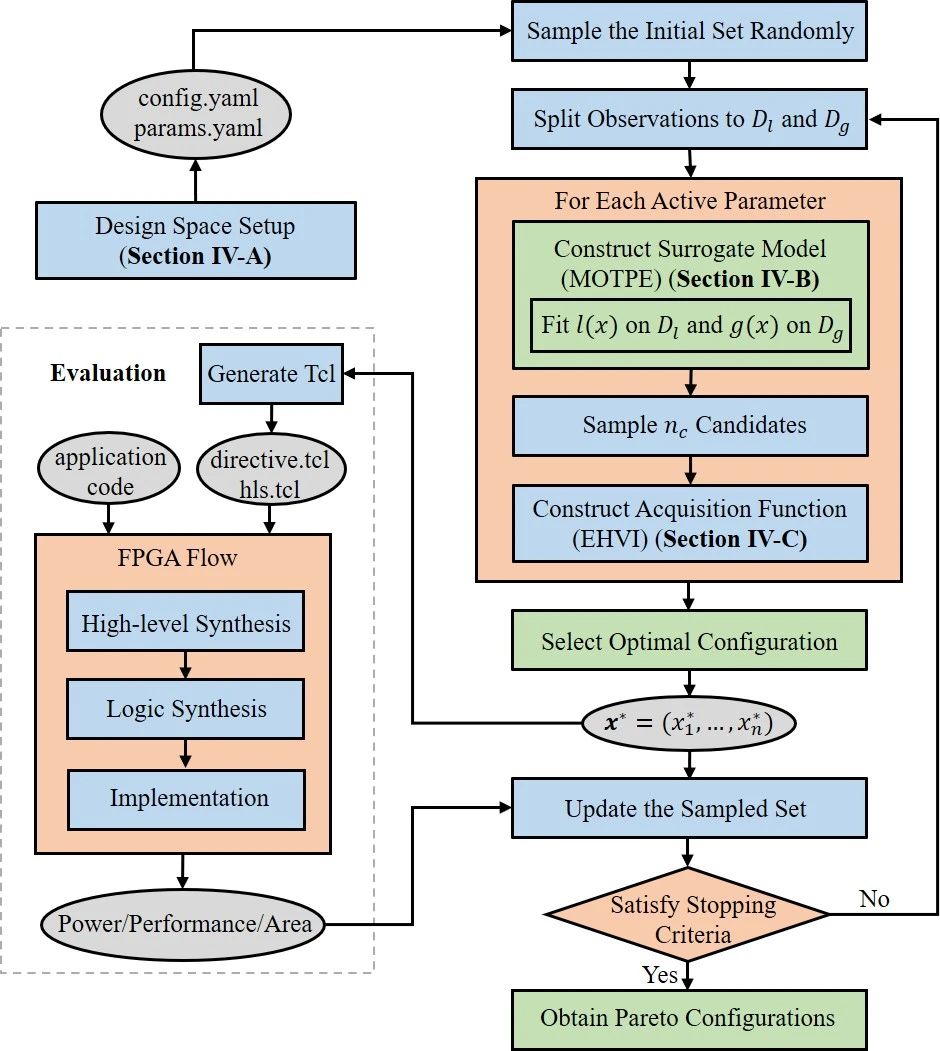
Fig. 3: The overall HLS design space exploration flow 2.4 DSE Results The quality of the circuit produced by HLS is measured by power, performance (latency, delay) and area, where area is reflected by resource utilization in FPGA including LUT, FF, DSP, BRAM, URAM and SRL with different weights. The PPA values are normalized to the default implementation of Vitis HLS to avoid inappropriate data shifting and to facilitate the convergence of the optimization process. Experiments are conducted based on the public MachSuite benchmark. Table 2 shows the characteristics of ten kernels from different domains. Each kernel contains several functions, loops and arrays, which can form a vast design space.
Table 2: Benchmark characteristics The proposed MOTPE with float encoding denoted as MOTPE-F, is compared with two meta-heuristic methods, SA and GA, which are widely applicable to HLS DSE. Besides, MOTPE-F is compared with the default implementation by Vitis HLS which has some automatic optimizations. To further validate the advantage of our float encoding method, we conduct DSE using MOTPE with discrete encoding additionally, represented as MOTPE-D, which encodes the directive parameter with discrete numbers to build the MOTPE model. The DSE algorithms are compared from two aspects with the corresponding results shown in Table 3: 1) The product of latency, power, delay and area (LPDA). 2) Average Distance from Reference Set (ADRS). Table 3: LPDA and ADRS comparison Four examples of the obtained Pareto fronts by three algorithms in Fig. 4 show the competitive performance of our MOTPE while the purple point represents Vitis HLS default implementation and the grey point represents dominated configuration. Our obtained Pareto fronts are much closer to the reference Pareto fronts than SA and NSGA-II.
Fig. 4: Pareto front comparison This paper presents a Bayesian optimization-based method with float encoding to address the DSE of HLS designs. The design space is modeled in a tree-structured manner to avoid invalid configurations efficiently. To model the non-linear mapping relationship between directives and objectives and the correlated relationship among power, performance and area, MOTPE is used as the surrogate model with multi-objective acquisition function EHVI. By conducting various experiments on MachSuite benchmarks, the results demonstrate that our method outperforms SA and NSGA-II, with LPDA gains of 66.30% and 41.25% respectively. The average ADRS is less than 0.1, showing the generality of our method for applications from different domains.
About ISEDA 2024
Jointly organized by EDA2 and EDA Committee of CIE, the ISEDA (International Symposium of EDA) is an annual premier forum dedicated to VLSI design automation. The symposium aims at exploring the new challenges, presenting leading-edge technologies and providing EDA community with opportunities of predicting future directions in EDA research areas. ISEDA covers the full range of EDA topics from device and circuit levels up to system level, from analog to digital designs as well as manufacturing. The format of meeting intends to cultivate productive and novel interchangeable ideas among EDA researcher and developers. Academic and industrial EDA related professionals who are interested in EDA's theoretical and practical research are all welcomed to contribute to ISEDA.
Advisors IEEE/CEDA, ACM/SIGDA Department of Information Science, National Natural Science Foundation of China (NSFC) Chinese Institute of Electronics (CIE) Steering Committee, Major Plan of “Fundamental Research on Post-Moore Novel Devices”
Organizers EDA Ecosystem Development Accelerator (EDA²) EDA Committee of CIE
Co-Organizers Xidian University Peking University Southeast University Tsinghua University
SUBMISSION for ISEDA 2024
Submission of Papers
Invited Talks: Need an abstract within one page Extended Abstract: 1-2 pages Regular Paper: 4-6 pages Follow the standard double column template: https://www.ieee.org/conferences/publishing/templates.html
Scan the QR code above or copy the link to
enter the submission system. CONTACT US
Scan the QR code above or copy the link to visit the conference homepage. Conference Secretary | Joyce Zhong Yu Huang | huangyu61@hisilicon.com
| 